Hypothesis
The roman pentagon dodecahedron an astronomic measuring instrument for determining the optimal sowing date for winter grain.
G.M.C. Wagemans
In the course of the years, several different theories have been formulated, that attempt to clarify what the dodecahedron was used for and what meaning, what significance they had in the society of that time. A satisfactory explanation is yet to be given. Up till now, some 90 specimen have been found in that part of Europe, that used to belong to the Northwesterly part of the Roman empire. The circumstances during which the items where found are unclear, but still, with some certainty one could determine that they were probably used from the first up to and including the fourth century BC. In two recent publications (R. Nouwen 1993 and B.H. Greiner 1995), a comprehensive outline has been given of all the known data concerning dodecahedrons and in which also all the existing theories are being dismissed, based on partially scientific analyses. Greiner mentions an astounding 27 different theories, theories that are often miles apart, for example a candlestick, dice, a bludgeon, a children’s toy, a geodetic measuring instrument, a sceptre head etc.
A new hypotheses
This article presents a new theory for the use of the dodecahedron, together with experimental support. Shortly summarized, my new theory can be described as followed: the dodecahedron was an astronomic measuring instrument with which the angle of the sunlight can be measured and thereby one specific date in springtime, and one date in the autumn can be determined with accuracy. The dates that can be measured were probably of importance for the agriculture. The sowing date of winter grain is important for the achievement of optimal produce. Therefore I anticipate that the dodecahedron would only be used in autumn time.
The functioning of the dodecahedron as a measuring device is based on the angle of the sun on the highest point of the day. In a calendar year, the earth travels completely around the sun (365 ¼ day). The angle of the earth opposite the sun changes during the year in a sinus rhythm. The sun gets to the highest position around June 21, when the sun reaches the tropic of Cancer (degree of latitude N 23°.27') and the lowest point will be reached around December 22, when the sun reaches the tropic of Capricorn. (degree of latitude Z 23°.27').
The vernal equinoctial point and the autumnal equinoctial point are at respectively March 21 and September 23, when the sun has reached the level of the equator. The angle which the sunlight makes with the earth is subjected to the degree of latitude where one is.
As an example, take the city of Maastricht, located at N 50°.52'. At March 12 and September 23, the largest angle which the sunlight makes with the earth in Maastricht, is 90° - 50°.52' = 39°.08'. On June 21, it is 90° - (50°.52'-23°.27') = 62°.35' and on December 22, it is 90° - (50°.52'+23°.27') = 16°.41'.
When one is able to determine the angle which the sunlight makes with earth, one is actually measuring the date quite accurately. According to my hypotheses, the use of the dodecahedron is based on this knowledge.
The working is as follows: the dodecahedron was placed on a horizontal plate on a sunny day in autumn. Thereupon, around noon, when the sun reaches its highest point of that day, one would measure the light falling through two openings opposite each other (see figure 1). Next, twenty measuring points would be examined for beams of light going through the hole. This all would be done according to a specific system.
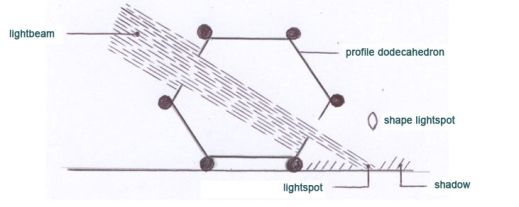
Figure 1
The last measuring point is obtained on the day that sunbeams fall through all the measuring points. In spring, the same measurements can be done (at the end of the measuring period, there will be no measuring point through which the light will fall through because the sun will be higher in the sky), but the hypotheses assumes that the dodecahedrons were only used in autumn.
Calculations
To be able to calculate the date accurately, one has to calculate the angles of the beams of sunlight which can be measured with the dodecahedron. When measuring the two holes opposite each other, is determined by the diameter of the dodecahedron and the average diameter of the two holes opposite of each other.
The angle straight through the two holes opposite of each other is the same for all dodecahedrons, namely 26,6°. As a result of which the angle can be calculated with the formula:
Angle of sunlight = 26,6° + Tg-1 | A + B (mm) |
A, B = the radius of the two openings, opposite each other.
D = diameter of the dodecahedron.
With this, the following should be marked: the calculation assumes that it concerns a perfect measuring body at which the small balls are fixed in such a way that the dodecahedron stands horizontally. In practice, this will probably not be the case, even though the smiths and bronze casters had the proper qualities available. For each dodecahedron, six different measuring points can be obtained (the twelve areas give six different combinations of two holes that are opposite each other.) With the six angles obtained, the corresponding dates can be determined.
This can be done through using formulas from astronomy but also through using charts.
When the degree of latitude is known, and the angle of the sunlight has been measured, one can determine the corresponding date by simply using the chart.
These calculations have been done with 29 dodecahedrons, with which for each dodecahedron the first and the last date has been determined.
The data necessary, like diameter, measurements, holes and the location where it was found, all come from the publication of Nouwen.
The number of 29 has not been established randomly. The following considerations have had an affect on this:
- first of all, the measurements are only useful when the finding place of the dodecahedron is known. After all, without the date concerning the degree of latitude, the calculation can not be done.
- Further, the dodecahedron has to be in an undamaged state, so that the diameter of all the twelve holes can be measured.
- Next, the current location of the dodecahedron has to be known, so that the angles that are calculated also can be calculated for this original specimen.
The results of these calculations are summarized in chart 1. The numbers of the chart correspond to the numbering from the publication of Nouwen.
Chart 1. Measuring period autumn
Nr | Vindplaats | Meetperiode |
1 | Bassenge | 31 aug. – 23 sept. |
4 | Bad Cannstatt | 27 aug. – 30 sept |
34 | Besançon | 4 sept.– 30 sept. |
55 | Camarthen | 14 aug. – 21 sept |
66 | Elst | 13 sept – 22 sept |
69 | Carnuntum | 2 sept – 9 okt. |
73 | Conches-dessous | 15 sept.– 26 sept. |
nr. 1 t/m 3 | = Belgium |
When studying the calculations, it appears that the total measuring range varies between August 10 and October 9. The last date varies between September 9 and October 9. Supposing that the dodecahedrons were used to accurately pinpoint a certain date, it will probably be the last date that can be measured accurately simply because a date measured after the desired date would have no function whatsoever. For example: the date which has to be recorded is September 25. Measuring the angle of the sunlight that is smaller than the angle which the sunlight makes on September 25, would mean that the desired date has passed. In order to avoid the risk that on the desired date the sky is clouded, several measuring points are needed in the period before the date is reached. When the user knew how many days there would be between the several different measuring points, the desired date could nevertheless be determined even when on that day the sky was cloudy.
Foundation hypotheses
Now that the outcome of the calculations indicates what the measuring range of the 29 dodecahedrons is, the question arises in what context these data could have had meaning. It seams logic to firstly examine to what extent the archaeological context can be of any help. Unfortunately this is unknown for most of the dodecahedrons. Nouwen reports that in merely 9 times, the archaeological context is known and with 33 specimen, they do not know the place of origin. Some websites give some vague information.
The sites are very diverse. Dodecahedrons are amongst others found in military camps (13), graves (3), near a sanctuary (1), in treasures (2) and as a river discovery (3).
How large the contrast is can be concluded from the fact that next to the presence in military camps, a dodecahedron was found as a grave offering in a woman’s grave.
The archaeological context offers little information about the possible meaning of the dates. Further, we can ask ourselves why the dates that can be measured were that important. It could be religious day or holiday. However, in such a case, the measuring range should be more focused around a certain date. This does not stroke with the findings as explained before.
Another possibility is to analyse the area of distribution further. There was not one dodecahedron found in the area around the Mediterranean sea: Italy, Spain and Greece.
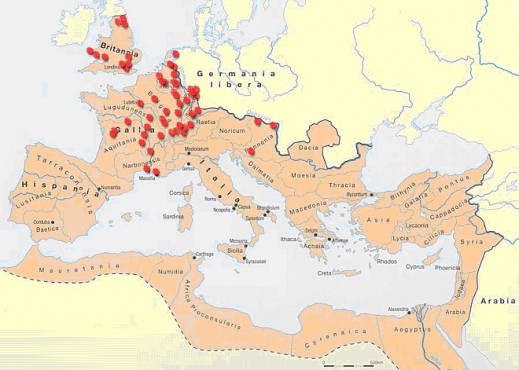
Dodecahedron sites
The findings were made after the first century AD and focus on the Roman or indigenous Roman fields.
These contemplations amongst others, motivated me to make a connection between the climate differences between the Mediterranean sea and North-western Europe which led to the link with agriculture.
An important difference in climate between North-western Europe and Southern Europe is mostly the hardness of the winter.
An accurate date definition is not necessary for harvesting, after all, they could see and/or feel the fruits and determine whether they were ready to be harvested.
Sowing does need to happen on a date that is most favourable for the crops so that the farmer can get the largest harvest. This is especially important for winter grains.
Nowadays, winter barley and winter wheat are being sewed in September/October. (see figure 2)
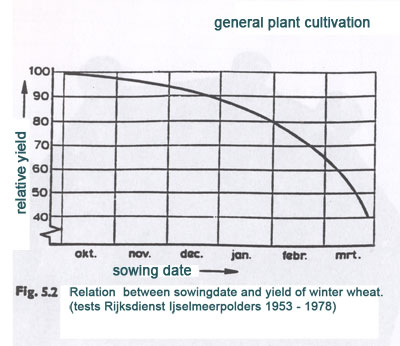
Figure 2
I am aware that caution is required when one interpreters the harvest results of the twentieth century with the results of the first centuries BC because differences can occur through corn refinement, new sorts of crops, a possible climate change, diseases and other differences.
As we can have concluded from the measurements, it seems that the last measuring point of the dodecahedron varies between September 9 and October 9. This corresponds with the results of tests done on crops that have been done in the twentieth century.
The sowing date for winter grains is extremely important for the following reasons:
- When the sowing is done to early, the plant will be developed too much and that can result in frost damage in wintertime.
- When the sowing is done too late, the roots of the plant can be underdeveloped and that can cause the plant to dehydrate, especially when frost and thaw alternate.
From a citation done by Plinius, one can conclude that even Roman farmers had problems with this. “ the crops have been nipped by an extremely cold winter, in March they actually sowed the field again, and had a bounteous harvest...”. That this has changed little through the centuries is shown in a citation about agriculture in the beginning of the nineteenth century “… it appears that they began sowing the winter grain; if the plants were affected by weather conditions, they would plough everything again and replaced it with summer grains, but that gave smaller yields...” The difference in yields can probably be explained due to the fact that the Roman farmer didn`t plough his field after the winter. This leads to the growth of grain plants that have survived the winter and in that way contribute to a larger yield.
From both citations, one could conclude that farmers preferred winter grains over summer grains. They considered summer grains as an extra guarantee for poor winter produce.
Only in case of urgency, at which the property isn’t available in autumn due to rotation of crops for example, summer grains could be chosen instead. Presumably, during the Roman time, they did not make a distinction between summer and winter grain so that they did not have to be nervous for mixing several sorts of grain. Grain refinement of summer and winter grain had is entry some time later.
I have to make one note concerning the sowing date: this was meant purely as an indication. The actual date on which the farmers would sow, depended of course on the weather conditions at that moment.
The archaeological context in relationship with the hypothesis
The most important indicator for the value of the hypothesis written by me, is the question whether the archaeological context fits in the hypothesis. Hereunder, a number of circumstances during the findings will be discussed.
The presence of a dodecahedron in the sanctuary (Schwarzenacker near Homburg/Saar) and as a river discovery (Nijmegen, Trier, Zürich) emphasize the possible relationship with religion.
The determination of the date of such an importance for the entire society will go hand in hand with religious ceremonies and it is therefore not surprising that dodecahedrons were found in a ritual context.
The presence of the dodecahedron in the treasure filled with coins (Membrey, Saint Parize-le-Châtel) , found in the grave of a wealthy woman and near a villa-rustica (Greiner says that 4 dodecahedrons were possibly found in a villa-rustica) prove that the dodecahedron was a possession of a wealthy person.
Considered that religious offices were occupied by the elite, it is not strange that these same people owned villas.
Approximately 13 dodecahedrons were found in places where military troops were stationed. If dodecahedrons were used in order to improve agriculture, this automatically means that Roman armies, or at least parts of it, were involved in agriculture and had to contribute to their own food supply.
This is being confirmed amongst others by Heinrich Krefeld, who wrote the following"...In den ruhigen Zeiten des 2. und 3. Jh wurde ihnen oftmals noch während ihrer Dienstzeit Ackerland in der nähe des Lagers oder Kastells zur Bebauung zugewiesen, das sie auch an ihre Söhne vererben konnten, wenn diese sich verpflichteten, ebenfalls Soldat zu werden ..."
For that matter, it is quite a logical thought that soldiers would help in food supply during peace time, and according to the quote mentioned above, it also guaranteed recruitment.
Whether the agricultural grounds round the Roman army stations where exploited by leaseholders or by the militaries themselves is not of significance, because it concerns large-scale exploitation of agricultural grounds directed from a central point.
The use of the dodecahedron could go together with dispersed land possession and with an attempt to optimize the yields.
The Julian calendar and the method of date determination
(for the origin of our current calendar, read this article)
An important discussion topic is the question why this method of date determination was used when the Julian calendar was already in use
At first, one could think that it is an instrument that was meant for the farmers because this group probably could not understand, and therefore used the Julian calendar.
When we compare the archaeological context of the dodecahedrons, we can find some degree of overlap of power, wealth and religion.
This was for the simple farmer but belonged to the upper class, from which we could expect that they have had a proper schooling and therefore could handle the Julian calendar.
An explanation could be that a date for agriculture would not be the same for the entire empire, which it would be with religious holidays, but it is a date which depends amongst others on the type of soil and climatologically circumstances, and therefore can differ from region to region.
By recording this date with the aid of a dodecahedron, and by announcing it each year from a central point (temple, military camp, villa-rustica etc.) for a certain agricultural area, confusion could be prevented. By announcing the proper sowing moment, and not connecting it to the Julian calender, it was possible that the farmers would be accepting it more easily, certainly when this would happen simultaneously with the worship of an important god for farmers. (see my hypothesis about the Gallo-Roman horse goddess Epona on this website, under the chapter other mysteries).
In the event that leaseholders had to give up a fixed part of the yields to a large landowner, he could easily use this as a method to register yields. This enabled him to determine the sowing date for his agricultural domain which would expect to have the highest yields and therefore would enable him to increase his income.
Special specimen
The dedecahedron of London
In the museum of London, a section of a dodecahedron (import nr C996) is being saved with at each vertex 3 little balls (see figure 3).
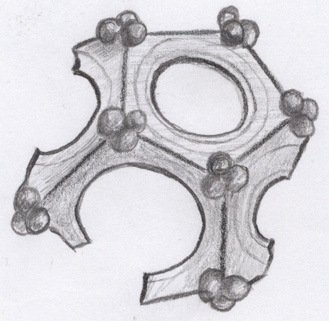
Figure 3
This can indicate that the small balls were the legs of the dodecahedron with which the device could be placed in different angles. This entirely matches with my hypotheses because the small balls would have had an important function. They were used to apply angle corrections because the dodecahedron was never casted completely symmetric. It is plausible that this method was applied to the first few dodecahedrons but were rapidly replaced by placing merely 1 small ball at each angle that can be of service for all three adjoining areas.
The icosahedron of Arloff (Rheinisches Landesmuseum, Bonn)
The icosahedron is an item that can be compared to the dodecahedron but is made out of 20 equilateral triangles by which only 12 angle points appear instead of 20 (see figure 4 and 5)
The icosahedron has only two areas that are opposite each other and have an opening. The small balls clearly have different diameters (two balls are missing).
Because we are dealing with a different geometrical shape, the angle of the heart of the two holes is 48,2° instead of. 26,6°(dodecahedron).
Because there are just two holes that are opposite each other, only one date will be possible.
The different diameters of the holes are the solution. Because the small balls of the surfaces that are next to the surfaces with two holes have different diameters, the two holes that are opposite each other can be placed in six different positions. This is shown in figure 6.
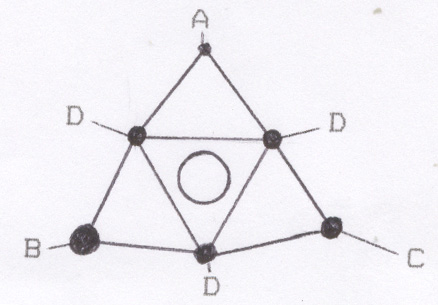
Figure 6
The small balls at the angular points of the surface with the opening will probably have the same diameters (D) while the balls on the angular points A, B and C will have different diameters. The surface of the other opening will have the same structure but the small balls will have other diameters.
Of the total of twelve balls, there will be a maximum of eight balls that have a different diameter.
As the diameters of the balls were not mentioned in the publication, the date cannot be determined. In theory, if we take three of the same balls (ball C is the same as D), the date will be August 30. Is the ball smaller than D, the date measured will be later than August 30. If the ball is larger, the date will be earlier.
Measuring original specimen
At first, I would like to thank dr. M. Brouwer (in 1997 conservator Roman archeology RMO Leiden) to make the dodecahedrons available. The dodecahedrons found in the Netherlands were taken out of the display specially for my research. I was able to do research for a total of three days.
As mentioned earlier, we can assume that the dodecahedrons were not casted completely accurate and it will therefore be possible that the calculated data in the schedule can differ with the data of the original specimen.
To investigate how large the differences could be, I conducted angle measurements in the Rijksmuseum of archaeology in Leiden with the dodecahedrons of Elst and Hartwerd (see figure 7 and 8).
Before discussing the results of the measurements, it is useful to clarify the variations that could occur with measuring.
With a perfect geometrically device, only six measurements will be possible. The dodecahedron has to meet the following requirements:
- The dodecahedron must have a perfectly geometrical shape.
- The heart of the dodecahedron must be exactly in the middle and the opening has to be perfectly round.
- The small round balls at the angular points have to be fixed in such a way that the dodecahedron can stand horizontally in every position.
If one or more of these requirements has not been met, a completely different situation will occur.
For every area that is pointed towards the sun, there are 5 different areas that are aimed at the ground. Therefore there are (12 times 5 =) 60 different angle measurements possible since there are 12 areas.
Because the results of the measurements will need to give information about the way the dodecahedron will be used, all 60 areas of the dodecahedron have to be recorded.
This determination will be performed with the aid of a spot of light (see figure 9)
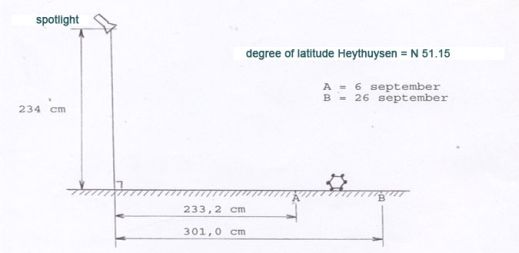
Figure 9
This method was used by myself for the calibrating of the replicas which I have made to found my thesis. For this reason, figure 9 is an example of the angle measurement of the degree of latitude of the town of Heythuysen. For every measuring point , the dodecahedron will be moved forwards or backwards till the point that a small spot of light is just visible. Thereupon, the distance between the spot and the perpendicular line beneath the light spot will be measured.
For point A and B, the date can be calculated:
Point A angle sunlight = Tg-1 | 234 mm | = 45°06’= 6 september |
Point B angle sunlight = Tg-1 | 234 mm | = 37°52’= 26 september |
because there are no identifying marks on the dodecahedron, I chose a method of numbering as in figure 10.
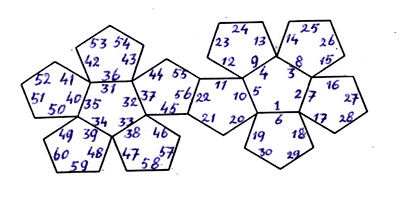
Figure 10
When numbering the measuring point, the position of the dodecahedron will be reflected at which the measuring will be done. The number will be above the opening of the area that is aimed at the sun during measuring.
In chart 2 and 3, the results of these measurements have been summarized.
Chart 2:
Hartwerd: total measuring range: 41°.57’ - 53°.39’
Nr. | Angle(°) | Nr. | Angle(°) | Nr. | Angle(°) | Nr. | Angle(°) |
18 | 41.57 | 28 | 45.09 | 15 | 46.14 | 1 | 49.58 |
44 | 42.42 | 2 | 45.13 | 34 | 46.17 | 25 | 50.24 |
56 | 42.48 | 20 | 45.25 | 5 | 46.22 | 13 | 50.38 |
27 | 43.24 | 37 | 45.31 | 41 | 46.52 | 59 | 50.58 |
22 | 43.50 | 7 | 45.32 | 50 | 46.57 | 42 | 51.03 |
10 | 43.58 | 33 | 45.33 | 46 | 46.58 | 12 | 51.08 |
14 | 44.05 | 17 | 45.34 | 26 | 47.05 | 19 | 51.44 |
58 | 44.11 | 8 | 45.44 | 57 | 47.14 | 49 | 51.47 |
3 | 44.24 | 6 | 45.45 | 11 | 47.28 | 48 | 51.52 |
45 | 44.24 | 54 | 45.52 | 43 | 47.41 | 51 | 52.07 |
31 | 44.26 | 4 | 45.55 | 36 | 48.31 | 32 | 52.49 |
40 | 44.29 | 55 | 45.56 | 30 | 48.57 | 39 | 53.02 |
47 | 44.47 | 29 | 46.03 | 23 | 49.21 | 60 | 53.03 |
16 | 44.48 | 35 | 46.07 | 52 | 49.25 | 24 | 53.31 |
38 | 44.48 | 21 | 46.11 | 53 | 49.31 | 9 | 53.39 |
Chart 3:
Elst: total measuring range: 35°.57’ - 45°.36’
Nr. | Angle(°) | Nr. | Angle(°) | Nr. | Angle(°) | Nr. | Angle(°) |
1 | 35.57 | 34 | 39.04 | 10 | 40.41 | 43 | 41.46 |
4 | 35.59 | 26 | 39.18 | 38 | 40.47 | 41 | 41.48 |
9 | 36.53 | 5 | 39.20 | 48 | 40.47 | 30 | 41.53 |
23 | 37.14 | 28 | 39.22 | 46 | 40.49 | 55 | 42.00 |
25 | 37.41 | 27 | 39.25 | 45 | 40.50 | 6 | 42.43 |
24 | 37.59 | 22 | 39.43 | 50 | 40.53 | 51 | 42.44 |
57 | 38.05 | 8 | 39.45 | 18 | 41.00 | 29 | 42.45 |
13 | 38.30 | 17 | 39.58 | 12 | 41.03 | 32 | 42.46 |
19 | 38.30 | 36 | 40.04 | 42 | 41.11 | 53 | 42.53 |
2 | 38.32 | 11 | 40.06 | 33 | 41.21 | 44 | 43.21 |
49 | 38.43 | 35 | 40.09 | 56 | 41.21 | 52 | 43.45 |
3 | 38.44 | 21 | 40.10 | 47 | 41.31 | 59 | 44.08 |
37 | 38.55 | 39 | 40.15 | 16 | 41.38 | 54 | 44.59 |
20 | 38.59 | 14 | 40.32 | 40 | 41.43 | 58 | 45.35 |
15 | 39 | 60 | 40.40 | 7 | 41.44 | 31 | 45.36 |
If we convert the measuring range of this degree of latitude to data, it will be shown that each dodecahedron has a measuring range of approximately 25 days
If we had started with theoretical measuring points with a perfect shape, the measuring range of the dodecahedron of Elst would have been notably smaller (see chart 4)
Chart 4:
A calculation based on a complete symmetry of the dodecahedron where a mere 6 dates would be possible (the areas opposite each other give the same date when aimed at the sun).
Nr. | Elst | Hartwerd |
1 | 13 sept. | 12 aug. |
2 | 18 sept. | 29 aug. |
3 | 19 sept. | 30 aug. |
4 | 21 sept. | 1 sept. |
5 | 22 sept. | 1 sept. |
6 | 22 sept. | 9 sept. |
The dodecahedron of Elst is not symmetric. This explains why the diameters of the holes are relatively little spread compared to other dodecahedrons. Nouwen writes about this and says "... with others, e.g Elst, one notices only variations between 13 to `18 millimetres..."
Using the dodecahedron
Because calculations show that the measuring period does not exceed 30 days in most cases (see chart 1) and mark signs on the areas are absent, I assumed that a method had to be used with which the measuring points should be selected with a fairly simple method.
When studying the dodecahedron of Elst, some small balls clearly had small areas (from wearing?) on the areas which they would have touched the ground while some small balls did not have this.
I should note that at the dodecahedron of Hartwerd, signs of restoration were present and that in one area, the edge of the opening was pushed inwards.
As well Nouwen as Greiner has noticed that almost every dodecahedron has the two largest holes exactly opposite each other. Greiner also states that these holes are probably fixed in the wax shape and that the core around in which the wax mall would be put, would be carved out at a later phase. These holes usually show damages or irregularities according to Greiner.
If we assume that it is for this reason that the two holes were not used as measuring points, 10 areas remain to determine a date, which means that there are a total of 50 angles that can be measured.
With these 50 remaining measuring points, I have found the following system what was used with the dodecahedrons. Of the remaining 50 measuring points, only 20 were used to determine a date.
It works as followed:
- Make a smooth horizontal area on which the measurements can be conducted at the time that the sun has reached its highest point of the day.
- Determine where the two largest holes of the two areas that are opposite each other are.
- Go and stand behind the horizontal area so that you are looking in the direction of the sun.
- Place the dodecahedron with one of the two largest holes faced down and turn the dodecahedron in such a way that there are 5 sloping areas on top and aimed towards the sun en check if there is a small spot of light present.
- Now turn the dodecahedron without lifting it up, in such a way that the 4 remaining areas can be checked. Write down or remember how many of the 5 measuring points have light passed through.
- Next, place the largest hole down and repeat the measurements. In total, there should be 10 measuring points checked.
- Now, place the dodecahedron in such a way that one of the two largest holes will be on the lower left side (on the side of the user) of the area where light should shine through.
- Check if there is a small spot of light present, and turn the dodecahedron round its imaginary axe that runs through the two largest openings and check the remaining 4 measuring points. The two areas with the largest openings that are opposite each remain at the same place with each measuring point. In total, 15 measuring points should have been checked.
- Next, place the other large opening in the same position and repeat the measuring as described in step 8. All twenty measuring points need to be checked.
The measuring seems quite difficult at first, but after some practice, the complete measuring can be done easily within 2 minutes.
I have noted that the small balls on the two surfaces of the largest opening of the dodecahedron of Elst had the most wear. This corresponds to the method of use in which these balls of the dodecahedron were turned without lifting them up.
According to my hypothesis, the dodecahedrons were used in autumn. That would mean that as the days passed by, the sun would stand lower and therefore there would be more measuring points that would pass through light.
The result of the measuring can be explained as followed:
If there would be 6 of the total 20 measuring points that would pass through light, then they would be (20-6=) 14 days away from the preferred date. Two days later, 8 of the 20 measuring points would let light through, and then they would be 12 days removed of the preferred date, and so on.
According to the method explained above, the following measuring points from chart 2 and 3 were used for the dodecahedrons of Elst and Hartwerd:
Elst:
The first large opening faced down: Nr. 1/17/20/58/59
Large opening opposite faced down: Nr. 31/41/25/24/44
Large opening left faced down: Nr. 5/21/47/60/7
Large opening opposite bottom left: Nr. 55/13/26/40/32
Hartwerd:
The first large opening faced down: Nr. 28/50/34/47/29
Large opening opposite faced down: Nr. 54/14/4/11/55
Large opening left faced down: Nr. 56/10/3/25/43
Large opening opposite bottom left: Nr. 17/30/38/35/51
As said before, the numbers of the measuring points of the two dodecahedrons differ because the first number has been placed randomly. The implementation of the measurements is for both dodecahedrons the same.
Naturally, there are a lot more variations possible with which 5 measuring points will be gotten each time. Based on the data which will be obtained with these two dodecahedrons, and the experience with my replica, with which the exact date can be determined quite accurately, the method as described above seems the most probable.
The data obtained through this method is summarized in chart 5 and 6.
Chart 5:
The results of the measuring of the dodecahedron of Elst (width N 51°.55').
date | angle sunlight (°) | angle measuring point (°) | deviation (°) | deviation in days |
3 september | 45.37 | 45.36 | - 0.01 | < 0.5 |
3 september | 45.37 | 45.35 | - 0.02 | < 0.5 |
8 september | 43.45 | 44.08 | + 0.23 | 1 |
9 september | 43.22 | 43.21 | - 0.01 | < 0.5 |
10 september | 43.00 | 42.46 | - 0.14 | 0.5 |
11 september | 42.37 | 42.00 | - 0.37 | 1.5 |
12 september | 42.14 | 41.48 | - 0.26 | 1 |
13 september | 41.51 | 41.44 | - 0.07 | < 0.5 |
14 september | 41.28 | 41.43 | + 0.15 | 1 |
15 september | 41.05 | 41.30 | + 0.26 | 1 |
16 september | 40.42 | 40.40 | - 0.02 | < 0.5 |
17 september | 40.19 | 40.10 | - 0.09 | 0.5 |
18 september | 39.56 | 39.58 | + 0.02 | < 0.5 |
19 september | 39.33 | 39.20 | - 0.13 | 0.5 |
20 september | 39.09 | 39.18 | + 0.09 | 0.5 |
21 september | 38.46 | 38.59 | + 0.13 | 0.5 |
22 september | 38.23 | 38.30 | + 0.07 | < 0.5 |
23 september | 38.00 | 37.59 | - 0.01 | < 0.5 |
24 september | 37.36 | 37.41 | + 0.05 | < 0.5 |
28 september | 35.58 | 35.57 | - 0.01 | < 0.5 |
The average deviation was 0.11 (11 minutes of arch). This corresponds to half a day. The largest deviation was a day and a half at the measuring point of September 11.
Chart 6:
The results of measuring of the dodecahedron of Hartwerd (width N 53°.04').
date | angle sunlight (°) | angle measuring point (°) | deviation (°) | deviation in days |
11 august | 52.11 | 52.07 | - 0.04 | < 0.5 |
17 august | 50.20 | 50.24 | - 0.04 | < 0.5 |
22 august | 48.41 | 48.57 | + 0.16 | 1 |
23 august | 48.21 | 47.41 | - 0.40 | 2 |
24 august | 48.00 | 47.28 | - 0.32 | 1.5 |
25 august | 47.40 | 46.57 | - 0.43 | 2 |
26 august | 47.19 | 46.17 | - 1.02 | 3 |
27 august | 46.58 | 46.07 | - 0.51 | 2 |
28 august | 46.37 | 46.03 | - 0.26 | 1 |
29 august | 46.16 | 45.56 | - 0.20 | 1 |
30 august | 45.54 | 45.55 | + 0.01 | < 0.5 |
31 august | 45.33 | 45.52 | + 0.19 | 1 |
1 september | 45.11 | 45.34 | + 0.23 | 1 |
2 september | 44.50 | 45.09 | + 0.19 | 1 |
3 september | 44.28 | 44.48 | + 0.20 | 1 |
4 september | 44.06 | 44.47 | + 0.46 | 2 |
5 september | 43.43 | 44.24 | + 0.41 | 2 |
6 september | 43.21 | 44.05 | + 0.44 | 2 |
7 september | 42.59 | 43.58 | + 1.01 | 3 |
8 september | 42.36 | 42.48 | + 0.12 | 0.5 |
The average deviation was 0.29 (29 minutes of arch). This corresponds to a day and a half. The largest deviation was three days at the measuring points of Sepember 7 and August 26.
The largest deviation with the dodecahedron of Hartwerd, obtained ad August 26, is a deviation of three days. This can be explained by damage and signs of restoration. The largest deviation of the dodecahedron of Elst is a mere 1.5 day at September 11.
The first two measuring points of both the dodecahedrons were probably meant as a run-up to the actual measuring period.
The last date (September 28) of the dodecahedron of Elst is probably a spare measuring point. That would mean that this measuring point could easily be adapted by moving up the date. It is actually possible to move up a date by enlarging one of the openings but it is not possible to reduce the size of a hole. The measuring is only accurate when three measuring points shed light. The measuring is only accurate when there are at least 3 measuring points that shed light whereas with the dodecahedron of Elst, the last measuring point has no function for the determining of the dates. The number of measuring points for the dodecahedron of Elst to get an accurate date determination is 19.
Example 1: imagine that the dodecahedron of Elst has 6 of its 20 measuring points shedding light. Then, they are 19-6 = 13 days away from the preferred date.
Example 2: imagine that the dodecahedron of Hartwerd has 9 of its 20 measuring points that sheds light. Then, they are 20-19 = 11 days away from the preferred date.
The optimal sowing date for winter grains according to the dodecahedron of Hartwerd (September 8) is 16 days earlier than according to the dodecahedron of Elst (September 24). For this, the general rule is being used that in the region of Friesland, the average winter period starts two weeks earlier than more southern parts of the country.
Calibrating replicas
I have used this method for the calibrating of my replica because the same method is used with both the dodecahedrons. The calibrating (angle correction) was done by rasping the small balls and/or enlarging the opening. It is possible that with the original specimen, the small balls were placed during the calibrating process and that could be because small corrections needed to be made at the holes.
This way, I have calibrated the dodecahedron for the period of 6 up to and including September 25.
With this replica I have showed that with a dodecahedron twenty unbroken days can be measured.
I have concluded that with the icosaëder, the balls had to be a lot larger than that I had expected. Corrections at the icosaëder can not be done by enlarging the holes because all 6 the measurements have to be done with only 2 holes opposite. Because one of the openings has a diameter of a mere 4.5 millimetres, the icosaëder can also be used on a different way. When using the dodecahedron, more and more measuring points should shed light as the date in the autumn approaches. When using the icosaëder, the accact opposite method can be used, so the number of measuring points that sheds light decreases. By using this method, the measurements of the small balls were the same as the original specimen of Arloff (visually).
When using the icosaëder, I have used the same measuring period, and I found that the difference in two successive measuring points was 4 days. Because the calibrating takes place in the winter period, I had to wait till that time for testing my replica. In autumn, I have tested my dodecahedron and I could determine the date quite accurately whereas the icosaëder had a deviation of one day. When using the icosaëder, the actual date is being determined by means of the magnitude of the light spot between two measuring points. When this spot of light is very small, then the date of the following measuring point has been reached. When there is a larger spot of light, they are some days (3 days at most) away from the following measuring point. Therefore, when using the icosaëder we got a deviation of one day. If the icosaëder would be calibrated with a two days difference between the measuring points, then an accurate date could be determined with a total measuring period of 10 days.
Ending
Now, I have shown that when using a dodecahedron, the preferred date can be determined accurately and that two specimen just having a small deviation after having been in the ground for about 1500 years would be cause enough for research to be continued by doing more measurements with more original specimen. Since I have accepted the theory that there are equal steps of just one day between the measuring points, the dodecahedrons of which the finding place and therefore the degree of latitude is unknown can be used for these measurements. The results of these last measurements can not be converted to a date but they are still valuable to substantiate the hypothesis.
We have to keep in mind that the dodecahedrons have been used over a period of about 300 years with which the method of using can have been different from time to time. The system as it has been used with the dodecahedrons of Elst and Hartwerd, does not have to be the system for all the dodecahedrons. In view of the many possibilities, I do think that the two largest opposite holes have played a large part in the measuring since there are no identifying marks to be found.
Eventually, we have to realize that only the user had to know the system and some of the users even took their secret to their grave, as can be concluded out of archaeological information.
Summary
In the course of the years different theories have been put forward which attempt to clarify what function the dodecahedron had or what purpose it served for the community of the time. These theories are often miles apart and speculate suchs things as a candlestick holder, dice, a sceptre head, a geometrical measuring device etc. A satisfactory explanation has yet to be given. According to my new theory the dodecahedron was an astronomical measuring device with which, based on the position of the Sun at its zenith (maximum elevation), in the Spring and Autumn a specific data could be determined. The data which could be measured was probably of importance for the farmers of the time and in particular the sowing date for winter grain was of extreme importance in order to achieve an optimal harvest yield. The influence an eventual harsh winter could have on the yield could the explanation for why the dodecahedra have only been found in North West Europe and not in Southern Europe. The task of recording/measuring these important dates was probably not left to the farmers themselves but would have been performed by a higher social class within the community because in the archaeological context there is a certain limit of overlap present between power, wealth and religion. The sowing date was in all probability separately determined from a central point for each agricultural region because depending on the type of soil and the climate conditions the date could differ per region. An important factor for the merit of my theory is that the icosahedron of Arloff, which has only two parallel faces with holes and has knobs on all the vertices with different diameters, also subscribe to this theory. Measurements of the dodecahedra of Elst and Hartwerd show that date determination is possible however the measurements performed were not complete. The investigation should therefore be continued using additional original examples to perform more measurements according to the methods as proposed in this paper.
Literature
Greiner,B.A.,1995. Römische Dodecaëder. Carnuntum Jahrbuch 1995. p.9/44.
Jong,J.A. de,1990. Algemene plantenteelt voor het middelbaar agrarisch onderwijs.
Meeus,J.,1982. Astronomical Formulae for Calculators, second edition, Enlarged & Revised.
Krefeld, H., 1963. Res Romanae.
Nouwen,R.1993. De Romeinse Pentagon-dodecaëder: mythe en enigma. Publicaties van het Gallo-Romeins Museum, Tongeren, Nr 45, Hasselt.
Philips,J.F.R., Jansen,J.C.G.M., Claessens,Th.J.A.H.,1965. Geschiedenis van de landbouw in Limburg 1750-1914. Maas-landse Monografieën.
Roymans,N.,1990. Tribal societies in Northern Gaul. An anthropological perspective.
Wagemans,G.M.C.,1996. Mysterie Romeinse Pentagon-dodecaëder ontsluierd? Westerheem, jaargang 45 no.4 p.199/207.
Wagemans,G.M.C.,1997. Was de Romeinse pentagon-dodecaeder een astronomisch meetinstrument voor het bepalen van de zaaidatum? Oudheidkundige mededelingen uit het Rijksmuseum van Oudheden te Leiden 77, 1997.



